Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Calculus I Exam Review

The first exam will cover chapter 4 of Stewart’s text, Single Variable Calculus, 6e except
for sections 4.6 and 4.8. Exam date is Tuesday, October 28 — start time is 7:45am, finish
time is 9:15am plus a 5-minute grace period. The exam will include several computational
problems and one proof. There will definitely be a question from section 4.5 asking you
to “put it all together” and a question from section 4.7. I may also explicitly ask for a
definition or theorem statement, though True-False type questions might also occur. The
chapter review provides a good source of problems for practice and consideration. As you
prepare for the exam, please remember the writing expectations that I have set forth.
Class-time on October 27th is devoted to your questions.

Definitions and facts to know

• absolute maximum, maximum value, absolute minimum, minimum value
• local maximum, local minimum
• limit at infinity and 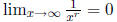for r > 0 a rational number.

Theorems to know

• Extreme Value Theorem
• Fermat’s Theorem
• Rolle’s Theorem
• Mean Value Theorem
• Closed Interval method

Computational problems

• Find critical points. Use the first derivative test and/or second derivative test determine
nature of a critical point.
• Compute limits at infinity to determine horizontal asymptotes.
• Sketch a function by method introduced in Section 4.5: find domain, x-intercepts,
y-intercept, symmetry, horizontal and vertical asymptotes, intervals of increase and
decrease, local maximum and minimum, concavity and points of inflection.
• Find the antiderivative of a polynomial and sin x and cos x

Proofs

• Prove Fermat’s theorem
• Prove Rolle’s Theorem
• Prove the Mean Value Theorem