NOTES ON CARDINALITY

When do two sets have the same size? As a simple example of the importance of this
question, imagine giving each of two young children a bag of candy. If they are not too
young, they may be quite concerned that one might have more than the other. If they
are not too old, they may not know how to resolve this problem. In fact, there is an
easy procedure to defuse the situation ?so easy that they can implement it themselves.
Namely, they can take candy from their bags one piece at a time, together, each putting
their portion aside in a pile. If they both run out of candy at the same time, they will
know that they got the same amount. Notice that they don't need to know how many
pieces each has, or even how to count. What they are doing is constructing a one-to-one
correspondence between their sets of candy, i.e. a bijective function from one bag of candy
to the other.

We take this idea as the basis of our definition of the size of a set, but we don't actually
define what size means. We only define what it means for two sets to have the same size.
We will call sets equivalent if they have the same size.

Definition. Let A and B be sets. We call A and B equivalent, and write A ~ B, if there
is a bijective function f : A → B. (We also say that A and B have the same cardinality.)

This idea is pretty evident, especially for finite sets. Here is an example involving
infinite sets. Let N = denote the natural numbers {1, 2, 3, 4, . . .}, as usual, and let S
denote the set of all perfect squares: S = {0, 1, 4, 9, 16, 25, . . .}. We will show that N ~ S.
To do this, we have to produce a function f : N → S, and prove that it is bijective. Here
is a function that does the job: f(x) = (x - 1)². First we notice that for every natural
number x, (x - 1)² is in fact a perfect square integer. Thus f really does map from N
to S. Let's prove that f is one-to-one. Consider two distinct natural numbers. Let x be
the smaller, and y the larger. Thus 1≤ x < y. Then 0 ≤ x - 1 < y - 1. Therefore
(x - 1)² < (y - 1)², and we have f(x) ≠ f(y). Now let's prove that f is onto. Let z be
a perfect square integer. Then there is an integer k such that z = k². Suppose first that
k ≥ 0. Then k + 1 ∈ N, and f(k + 1) =((k + 1) - 1)² = k² = z, and hence z is in the
range of f. If k < 0, then z = k² = (-k)², and -k > 0. By what we just proved, z is in
the range of f. Thus in all cases, z is in the range of f. Therefore f is both one-to-one
and onto, so it is bijective. Thus N ~ S.

At first this may seem a little odd -we might not want to believe that N and S have
the same size, because S looks like a fairly sparse subset of N. No one would argue that S
is not a sparse subset of N. Some people might try to argue with our definition of having
the same size, since it requires that we accept that S and N have the same size. We won't
even bother asking such people what definition they would like to use. The definition
above is a standard part of mathematics, and we need to understand how to use it and
what are its consequences. The basic fact is that it is possible for a set to be equivalent to
a proper subset of itself; S and N are just one such example. (The text reproduces a bit
of dialogue written by Galileo illustrating just this point, on pages 205-6.)

Here is another example, perhaps the simplest possible example, of a set that is
equivalent to a proper subset: N ~(N ∪ {0}). You ought to write down a bijective
function for yourself. In fact, there are many examples on the sheet Problems E -Section
6.1 in a link on the homework page of the course website, and you should write out solutions
to as many as you can.

The most basic properties of equivalence of sets are given in Lemma 6.1.1 in the text.
We reproduce the lemma here.

Lemma. Let A, B and C be sets.
(i) A ~ A.
(ii) If A ~ B then B ~ A.
(iii) If A ~ B and B ~ C then A ~ C.

Here is a proof of part (iii). You should write out proofs of parts (i) and (ii) yourself. (All
parts have easy proofs.) For part (iii), we assume that A~ B and B ~ C. Thus there
are bijective functions f : A → B and g : B → C. Then both f and g have an inverse.
Consider the function h = g o f : A → C, and the function k = f ^-1 o g^-1 : C → A. We
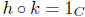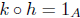easily check that and . Thus h : A → C has an inverse, and hence is
bijective. This proves that A ~ C.

This lemma can be useful. It can help us prove that two sets are equivalent without
producing an explicit bijection between them. For a very simple example, consider the
equivalence N ~ S proved above. We also claimed that N ~ (N∪ {0}) (and left the proof
as an exercise). By part (ii) of the lemma we know that S ~ N. Then by part (iii) we
know that S ~ (N∪ {0}). We don't need to write down a bijection from S to N∪ {0} in
order to know that there exists one.

Here are some familiar terms, with precise mathematical definitions using the notion
of equivalence.

Definitions.

1. The set A is finite if there is n ∈ N such that A ~ {1, 2, . . . , n}, or if A =Ø.
2. The set A is infinite if it is not finite.
3. The set A is countably infinite if A~ N.
4. The set A is countable if it is finite or countably infinite.
5. The set A is uncountable if it is not countable.

The term countable is just a convenient way of describing sets that are equivalent to a
subset of N, without mentioning whether or not they are infinite. Here are a couple of
examples of countably infinite sets: N, Z, S, the set of even integers, the set of odd
integers. More surprising is the fact that Q is countable. We will see the proof shortly.

It is a theorem, which we will not prove, that if m, n ∈ N and m ≠ n, then
{1, 2, . . . ,m} and {1, 2, . . . , n} are NOT equivalent. This is no surprise, of course, but
it does need a proof. For the purposes of this course, such a proof is a bit too fussy. We
will take it as granted that this theorem is true. (A proof is given in chapter 8 of the
text.) Given this, we can define the size, or cardinality, of a finite set as the unique natural
number n such that the set is equivalent to {1, 2, . . . , n} (or 0, if we are talking about the
empty set).

The notion of countably infinite set has a simple intuitive meaning that is clear when
you think of what a bijection from N to A means. If f : N → A is a bijection, we can
call f(1) the first element of A, f(2) the second element of A, and so on: f(n) is the
nth element of A. What we are doing is listing the elements of A. We can visualize the
bijection by writing the elements of A underneath the corresponding elements of N:

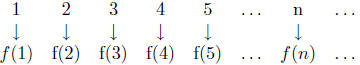
The point is that if you can "list" the elements of a set, then the set is countable (it
is finite if the list stops, otherwise it is countably infinite). For example, the fact that the
set of perfect squares is countable can be shown by listing its elements:

0, 1, 4, 9, 16, 25, . . .

This is shorthand for a more complete display, such as

which is itself an indication that there exists a bijection from N to S. We will use such a
listing, if it clearly indicates a complete listing, as a proof of countability. Now we'll show
how to give such a listing of Q. In fact, we will only do this for the positive rationals, .
(That isn't really any less surprising than the existence of a bijection of N onto Q.) The
proof, using this, that N ~ Q is an exercise.

Here is how the proof goes. First, for each natural number n, we list all the positive
rationals that can be written with denominator n. This will give a list of lists:

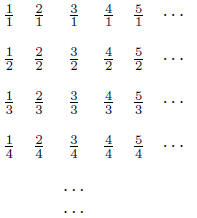
Now consider the diagonals in this array that start at an entry on the lefthand edge, and
continue up and to the right. We start at the upper left corner, and list these diagonals.
Each diagonal is itself a finite list. If we put these finite lists together we obtain a single
list containing all entries in the above array:

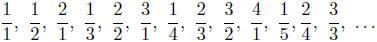
It is clear that every positive rational number occurs in this list. The problem is that some
(in fact, all) occur infinitely often. To fix this, we remove duplications — go through the
list and cross out each number that has already appeared:

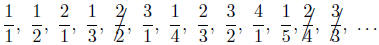
Removing the crossed-out entries leaves us with a list that contains each positive rational
number once and only once. As we described above, such a list indicates the existence of
a bijection from N to .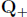

Many people find it hard to accept the fact that N and Q have the same number of
elements. After all, not only is N a very sparse subset of Q, but as we usually visualize
numbers on a line, the rationals seem to fill up the entire line, whereas the natural numbers
form a very discrete sequence of points. Of course, we know that the rationals don't fill up
the number line —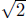 is a real number that is not a rational number. Most people who
have been exposed to some mathematics also know that π is not a rational number (but
the proof that π is irrational is pretty hard!). One might be tempted to conjecture that
since Q is really no bigger than N, then probably R is no bigger than Q. Actually, most
people would not even raise the question: what could be "bigger" than infinity? The truth
is that there are different sizes of infinity (in fact, there are infinitely many different sizes
of infinity). We have indicated this answer earlier by introducing the term uncountable
for sets that are not countable, i.e. that cannot be listed. The set of real numbers is an
example of such a set, as was proved by Cantor in the 19th century. His proof has become
a model for proofs in many areas of mathematics; it is truly ingenious. I feel that Cantor's
discovery is one of the triumphs of human civilization, like the discovery that Saturn has
rings, or that the earth moves around the sun.

Here is the proof. It is a proof by contradiction: we suppose that there exists a
bijection f : N → (0, 1), and we deduce a contradiction. (We know (by one of the exercises
on the problem sheet E, for example) that R ~ (0, 1), so it is enough to prove that N
is not equivalent to (0, 1).) Each number in (0, 1) can be written as an infinite decimal,
and we will use these decimal representations. Of course, some numbers have two decimal
representations. These are precisely the rational numbers that can be expressed as a
fraction having denominator equal to a power of 10. For example,

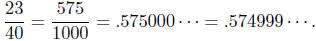
If we agree to not use a decimal representation that ends in an infinite sequence of 9's,
then each real number will have one and only one decimal representation.

Now consider the decimal representations of f(1), f(2), . . .:
 

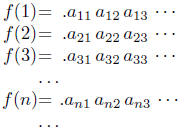
We consider the "diagonal" entries: 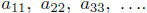(That is, we consider the
first digit of f(1), the second digit of f(2), and so on.) We build a new real number,
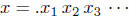, in the following way. For each n, let

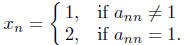
Then x is a real number in (0, 1) — it's decimal expansion consist only of 1's and 2's.
Moreover, x is not in the range of f. To see this, notice that by the way each 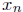is defined,
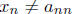. If x were in the range of f, then there would be a natural number k such that
f(k) = x. But then we would have 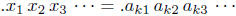. In particular we would
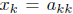have . But 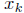was chosen precisely so that this does not happen. Therefore x
is not in the range of f, so that f is not surjective, contradicting our initial assumption.
Thus there does not exist a bijection between N and R. There are many, many more real
numbers than rational numbers.