Linear Algebra
9.3 Rotation matrices
Here's our old example of rotating coordinate axes.
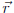= (x, y) is a vector.
Let's
call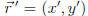 
the vector in the new coordinate system. The two are
related by
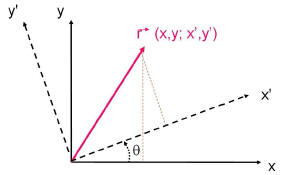
Figure 1: Rotation of coordinate axes by θ.
the equations of coordinate transformation we discussed in week 4 of the course.
These may be written in matrix form in a very convenient way (check):
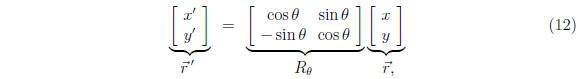
where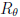 
is a rotation matrix by
θ. Note the
transformation preserves lengths
of vectors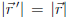 
as we mentioned before. This means the rotation matrix
is
orthogonal:
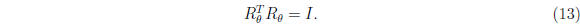
These matrices have a special property ("group property"),
which we can show
by doing a second rotation by θ':
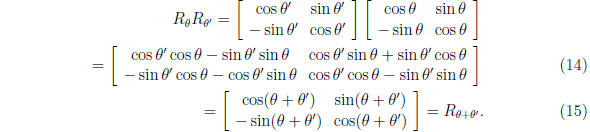
Thus the transformation is linear. More general def.
.
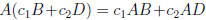9.4 Matrices acting on vectors
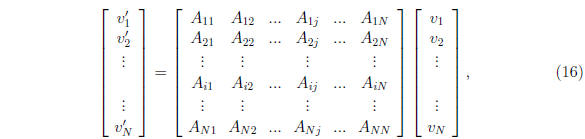
or more compactly
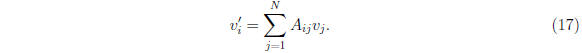
Another notation you will often see comes from the early
days of quantum mechan-
ics. Write the same equation
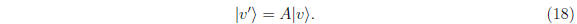
So this is a "ket", or column vector. A "bra", or row
vector is written as the adjoint
of the column vector:
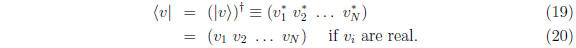
N.B. In this notation the scalar product of
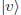and 
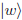is
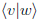, and the length
of a vector is given by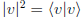 
.
9.5 Similarity transformations
Suppose a matrix B rotates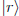 
to
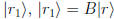. Now we rotate the
coordinate
system by some angle as well, so that the vectors in the new system are
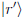and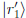 
e.g.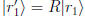 
What is the matrix which relates
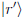to 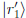i.e. the transformed
matrix B in the new coordinate system?
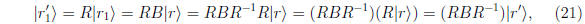
so the matrix B in the new basis is
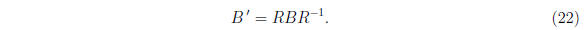
This is called a similarity transformation of the matrix
B.
To retain:
• similarity transformations preserve traces and determinants: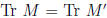
,
detM = detM'.
• matrices R which preserve lengths of real vectors are called orthogonal, RRT =
1 as we saw explicitly.
• matrices which preserve lengths of complex vectors are called unitary. Suppose
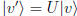, require 
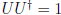, then
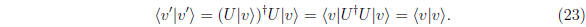
A similarity transformation with unitary matrices is
called a unitary transfor-
mation.
• If a matrix is equal to its adjoint, it's called self-adjoint or Hermitian.
Examples
1.
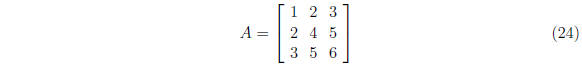
is symmetric, i.e. A = AT , also Hermitian because it is real.
2.
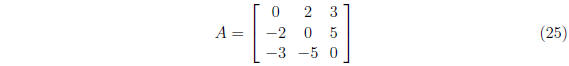
is antisymmetric, and anti-self-adjoint, since
.
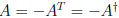3.
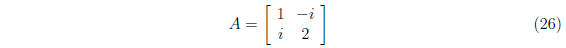
is Hermitian,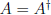 
.
4.
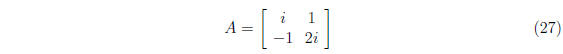
is antiHermitian,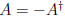 
. Check!
5.
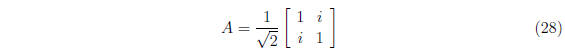
is unitary,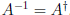 
.
6.
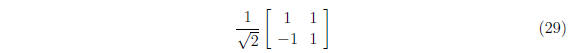
is orthogonal, A-1 = AT . Check!
9.5.1 Functions of matrices
Just as you can define a function of a vector (like
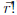), you can define a
function
of a matrix M, e.g. F(M) = aM2 + bM5 where a and b are constants. The
interpretation here is easy, since powers of matrices can be understood as
repeated
matrix multiplication. On the other hand, what is exp(M)? It must be understood
in terms of its Taylor expansion,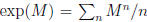 
!. Note that this makes no
sense unless every matrix element sum converges.
Remark: note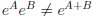 
unless [A,B] = 0! Why? (Hint: expand both sides.)