Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

OBJECTIVES FOR THE MMPT

NO CALCULATORS ARE ALLOWED ON THE MMPT.

PRACTICE THE FOLLOWING EXERCISES WITHOUT A CALCULATOR.

. Hierarchy of Operations

Be able to:
• apply the proper order of operations when evaluating an arithmetic expression
Ex. Evaluate: −3² − (−5²) − (−10)² = ;

• apply the proper order of operations when working with algebraic expressions.
Ex. Simplify: ;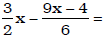

B. Factoring

Be able to factor polynomials over the integers:
1. By factoring the GCF

Ex. 25x (2x − 3)² − 5x (2x − 3) = ;

2. By regrouping of the terms
Ex. Factor completely: 16x³ − 4x² − 36x + 9 = ; x² − 2xy + y² − 4z² =;

3. By applying the basic identities:

• A² ± 2AB + B² = (A ± B)²
Ex. Factor: x² − 6xy + 9y² =
• A² − B² = (A + B)(A − B)
Ex. Factor: 16x⁴ − 81y⁴ =
• A³ ± B³ = (A ± B)(A² 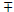AB + B²)
Ex. Factor: 27a³ − 64b³ =

C. Rational Expressions

Be able to:
• Simplify, multiply, divide, add and subtract rational expressions

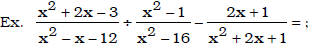
• Simplify complex fractions.

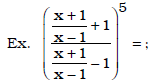
D. Exponents and Radicals

Be able to:
• Apply the laws of exponents to simplify, multiply and divide expressions involving
integer and/or rational exponents

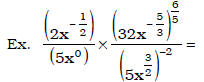
• Evaluate numbers raised to rational exponents and which result in a rational number

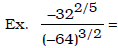
Write in radical form expressions containing rational exponents and simplify the
answer.

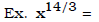(Answer :)

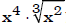• Write in exponent form a radical expression and simplify the answer.

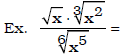(Answer :)

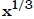Apply the laws of radicals to simplify, add, subtract, multiply and divide radical
expressions

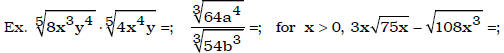
• Rationalize numerators or denominators.

Ex. 1. Rationalize the numerator: ;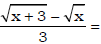
2. Rationalize the denominator and simplify: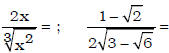

E. Equations

Be able to solve:

• linear equations

Ex. Solve for x: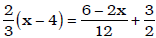

• quadratic equations by factoring

Ex. Solve for x: x² − 5x + 6 = 0 ;

• quadratic equations over the complex numbers using the quadratic formula

Ex. Solve for x: 3x² − 2x +1 = 0 ;

• polynomial equations over the complex numbers by factoring

Ex. Solve for x: x³ − 27 = 0 ;

• rational equations
Ex. Solve for x: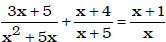
;
• absolute value equations

Ex. Solve for x: |2x − 3|= 5;

• equations in quadratic form

Ex. Solve for x: (2x + 3)² − 3(2x + 3) + 2 = 0 ;

• equations that involve radicals

Ex. Solve for x: ;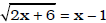

• exponential equations
Ex. Solve for x: ;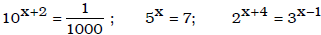

• logarithmic equations

Ex. Solve for x: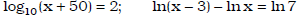

• literal equations

Ex. Solve for W: S = 2LW + 2LH + 2HW;

• systems of equations in two variables

Ex. Solve the system:

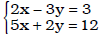
• trigonometric equations
Ex. Solve for x: 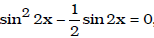, for 0 ≤ x ≤ 2π

F. Inequalities

Be able to solve:

• linear inequalities in one variable

Ex. Solve for x: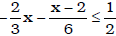

• compound inequalities

Ex. Solve for x: −4x ≤ 8 and 2(x − 3) > 4 ;

−4x ≤ 8 or 2(x − 3) > 4; −3 < 5 − 2x ≤ 10;

• absolute value inequalities

Ex. Solve for x: |2x – 3|< 5; |5x + 7| + 8 > 11;

• quadratic inequalities

Ex. Solve for x : x² − 5x + 6 ≥ 0;

• easily factorable or already factored polynomial inequalities

Ex. Solve for x: 2x³(x − 2)(x + 4)²(x +1) ≥ 0 ;

• rational inequalities
Ex. Solve for x: 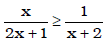.