Fri 5 Dec — Review for Final Exam (Appendix and Cpt 1)
Final is in 100 Smith Hall on Fri 12 Dec at 1:30 pm.
There are 15 multiple choice questions and 6 fill-in. The MC get no partial
credit but the fill in do.
In the MC questions, work out the solution, circle the answer on the test sheet,
and fill in the bubble
on the answer sheet.
In the MC, some of the questions are set up to make it difficult to guess. For
example a question
might read:
Solve x2+ 5x + 6 = 0. Then, add the two answers to get one of the following:
a. –1
b. 2
c. –5
d. 6
e. None of these.
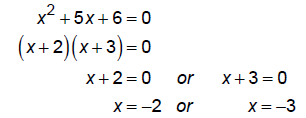
So, you would add –2 + (–3) to get –5. Circle choice C and fill in the bubble
on the answer sheet.
Check my web site for the finals and keys from Spring 2003 and Spring 2005. I
did not write those but
they are good practice for mine.
Now, let’s do some review from the Appendix and Chapter 1.
A.2 Geometry Essentials
Be sure to memorize the formulas in this section.
Pythagorean Theorem
Geometry formulas (area, perimeter, volume)
Congruent and similar triangles
Similar triangles - they are the same shape (the angles are the same but the
lengths of the legs
can be different).
The corresponding sides of similar triangles are proportional.
For example, given these triangles:
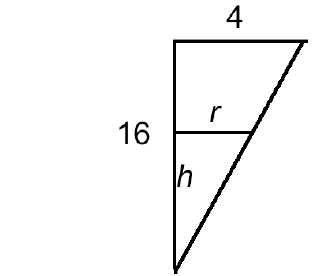
The two are similar since all the angles are the same. So, we can write the
following proportion:
4/r = 16/h
We could then solve for r in terms of h or h in terms of r.
A.3 Polynomials
Definitions
Factor using FOIL (First, Outer, Inner, Last)
Special product formulas (difference of squares, square of binomial, sum and
difference of
cubes)
Divide polynomials using long division
Factor polynomials
A.5 Rational Expressions
Reduce
Be sure to factor first and then cancel common factors.
Multiply and divide
Add and subtract
Find LCD and then combine:
EX: Combine into a single fraction: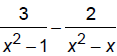
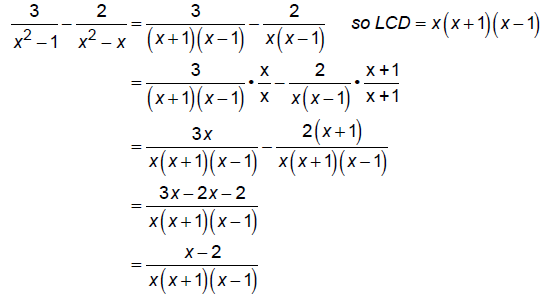
Complex rational expressions
A.6 Solving Equations
Linear
Quadratic and higher order
Solve: x4 = 2+x2
Let u = x2
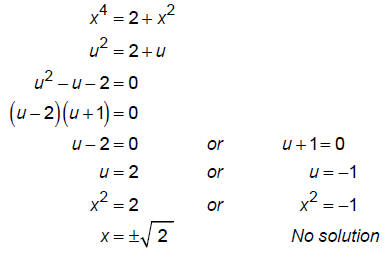
Absolute value
Complete the square
Quadratic formula
A.8 Problem Solving: Interest, Mixture, Motion Applications
Translate Verbal Descriptions into Mathematical Expressions
Simple Interest Problems
Mixture Problems
How many gallons of a 25% acid solution must be mixed with 5 gallons of a 10%
solution to obtain
an 18% solution?
Let x = # gal of 25% solution
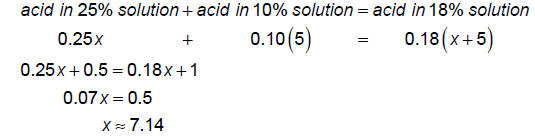
Uniform Motion Problems
Constant Rate Job Problems
A.10 nth Roots; Rational Exponents; Radical Equations
Simplify radicals
Simplify: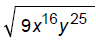
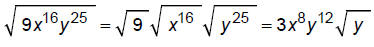
Add and subtract radicals
Simplify: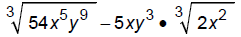
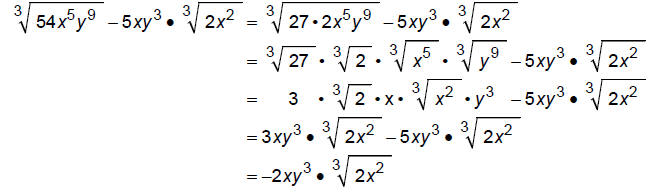
Rationalize denominators of radicals
Solve radical equations
Rational exponents
Simplify:
1.1 Rectangular coordinates; Distance & Midpoint Formulas
Rectangular (xy)
coordinates
Distance formula
Midpoint formula
1.2 Graphs of Equations in Two Variables
Graph equation by plotting points
Intercepts of a graph
Test for symmetry with respect to xaxis,
yaxis,
and origin
Symmetric with respect to x-axis: f(x) = -f(x)
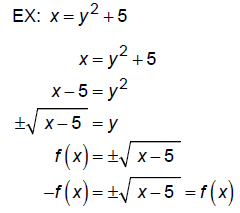
Symmetric with respect to y-axis: f(x) = f(-x)
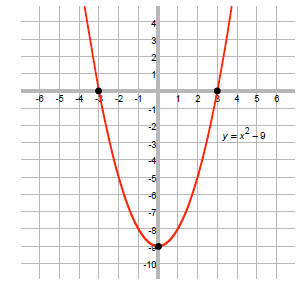
EX: y = x2-9
f(x) = x2-9
f(-x) = (-x)2-9
= x2-9
= f(x)
Symmetric with respect to origin: f(x) = -f(-x)
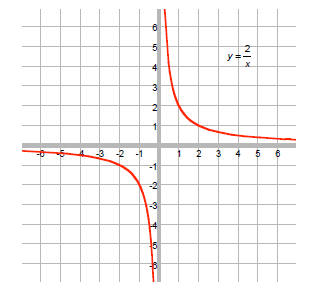
EX: y = 2/x
f(x) = 2/x
f(-x) = 2/-x
= -2/x
= -f(x)
1.3 Lines
Calculate and interpret the slope of a line
Graph lines given a point and the slope
Equation of a vertical line
Equation of a horizontal line
Pointslope
form of a line
Find equation of a line given two points
Slopeintercept
form of a line
Identify slope and yintercept
of a line given its equation
General form of a line
Parallel lines
Perpendicular lines
Find the equation of a line that passes through the point (5, 0) and which is
perpendicular to the
line that passes through (2, 3) and (1, -5).
First, find slope of the line that passes through the points (2, 3) and (1, -5):
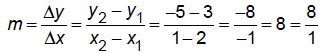
The perpendicular slope is m⊥= negative reciprocal =
-1/8
Now, use y = mx + b to find b.
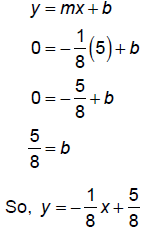
1.4 Circles
Standard form
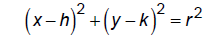
Graph a circle
General form and completing the square
Find the center and radius of the circle described by: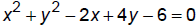
Put this in standard form by completing the square of both x and y.
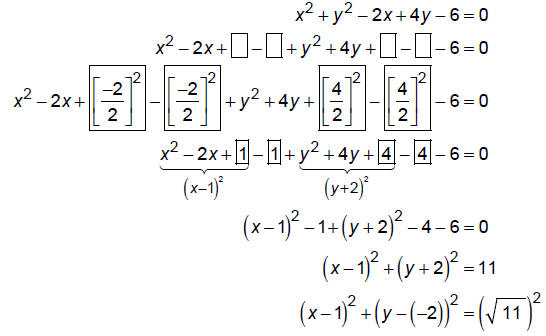
The center is (1, –2) and the radius is sqrt(11) .


