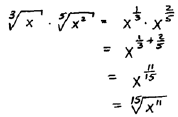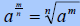Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Exponents

Rational, or fractional exponents, indicate that we have a radical expression. They are
intimidating at first but we should quickly get used to working with them. Basically, the
denominator is the root and the numerator is the exponent.

Rational Exponents – For any real number a and integer m and n > 1,

A. Rewrite the radical expression using rational exponents.

The above instructions did not ask to simplify, just rewrite using rational exponents.

B. Convert to a radical then simplify.

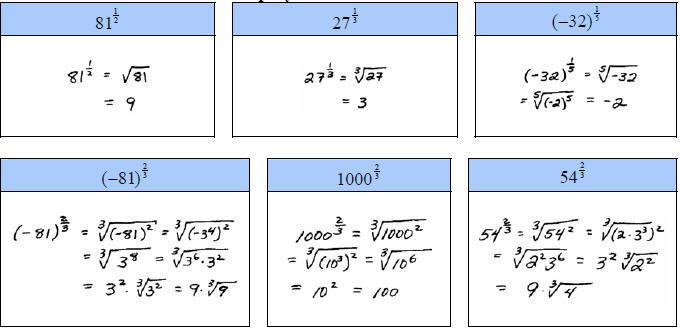
When variables are involved, many texts will say that all of them are assumed to be
positive to avoid the principal n^th root problem and absolute values. We can do the
following types of problems in a number of ways.

Often simplifying using the rules of exponents first is the easiest method but sometimes
converting to a radical first can simplify things, both methods yield the same result.

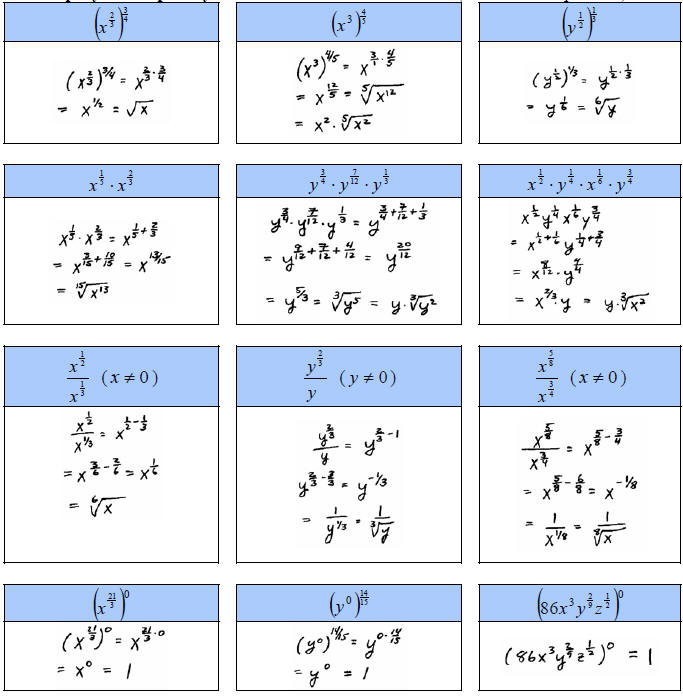
C. Simplify and express your answer in radical notation. (variables are positive)

Notice that in the above problems they all worked out nicely because the exponents were
multiples of the root. This is not always the case as illustrated below.

Tip: A quick way to simplify radicals is to divide the root into the exponents. This will
tell us what the exponent of the base should be outside the radical and the remainder will
be the exponent of the base inside the radical.

All the rules of exponents hold true when working with rational exponents. For example,
when multiplying we add exponents, but the exponents in this section are fractions.

D. Simplify and express your answer in radical notation. (variables are positive)

Sometimes we will be asked to multiply radicals with different roots but the arguments
will have the same base. This may seem impossible at first but it can be done as follows: