Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Factoring Polynomials

• To factor a polynomial means to write it as a product of other polynomials.
• A polynomial is prime if it cannot be written as a product of other polynomials.
• A polynomial is factored completely if it is written as a product of prime factors.

• First rule of factoring : use the distributive property to factor out the greatest common factor
• examples :

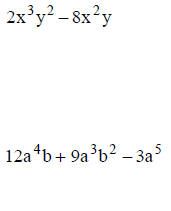
• Special factorization formulas
• Square of a binomial a² +2ab+ b² = (a + b)²
• Square of a binomial a² − 2ab+ b² = (a −b) ²
• Difference of squares a² − b² = ( a +b)( a − b)
• Sum of cubes a³ + b³ = (a +b)( a² −ab + b² )
• Difference of cubes a³ − b³ = (a − b)(a² + ab +b² )

• examples :

4x² − 64y²

8a³ + b³

4a² −12ab+9b²

• Use trial and error (reverse the FOIL process) to factor trinomials of the form ax² + bx + c
• examples :

x² − 6x + 8

2x² − x − 6

12x² −11x − 5

• Four terms - try factor by grouping
• example :

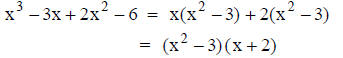
• examples :

8x³ + 2x −12x² − 3

x³ − x² − 4x + 4

• Be sure to factor each polynomial completely.
• examples :

12x² − 22x + 6

27a⁴b − 8ab⁴