Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Linear Inequalities

Overview
• Section 2.7 in the textbook:
– Graphing inequalities on a number line &
interval notation
– Using the Addition Property of Inequality
– Using the Multiplication Property of Inequality
– Solving inequalities using both properties

Graphing Inequalities on a
Number Line & Interval Notation

Solution Set
• Solution set – all values that satisfy an
inequality
• Often a solution set is expressed using a
number line

Graphing Inequalities on a Number
Line
• Consider the inequality x > 1
–What are some values of x that make the
inequality true?

• {2, 3, 4, 5, …}
– Thus x can be any value greater than 1

• Which direction on the number line indicates
increasing values?
– Can x = 1 be a solution to the inequality?

• Since x = 1 is not in the solution set, we put a
parenthesis around 1 on the number line

• Now consider x ≥ 1
– Graphed ALMOST the same way EXCEPT

• Is x = 1 included in the solution set?
– Since x = 1 is part of the solution set, we put a bracket around 1
on the number line

• Given x < a or x > a:
– Parenthesis goes around a on the number line (not
inclusive)

• Given x ≤ a or x ≥ a:
– Bracket goes around a on the number line (inclusive)

Interval Notation
• Easy once the graph is obtained

• Represents the “endpoints” of the graph
– First “value” is what is shaded furthest to the
left on the graph
– Second “value” is what is shaded furthest to
the right on the graph
– A shaded arrow represents ∞

• Parentheses ALWAYS go around infinity

Graphing Inequalities on a Number
Line & Interval Notation (Example)
Ex 1: Graph on a number line AND write in
interval notation:

a) x < -3
b) y ≥ 9⁄2

Addition Property of Inequality
• Works the same way as the Addition
Property of EQuality

• When a number is being added or
subtracted to the variable:
– Add the OPPOSITE number to BOTH SIDES

• Consider 2 < 7
–What happens when we add 2 to both sides?
–What happens when we subtract 5?

Addition Property of Inequality
(Example)
Ex 2: Solve, graph, AND write the solution
set in interval notation:

a) x + 3 > 4
b) 3y – 4 ≤ 2y – 9

Multiplication Property of Inequality
• ALMOST the same as the Multiplication
Property of EQuality

• When the variable is being multiplied by a
number:
– Divide BOTH SIDES by the number
INCLUDING THE SIGN

• Consider 4 > 2
–What happens when we divide by 2?
–What happens when we divide by -2?

• Thus, when we DIVIDE an INEQUALITY
by a NEGATIVE number:
– Switch the direction of the inequality
– Failing to SWITCH the inequality when
DIVIDING by a NEGATIVE number is a
common mistake!

Multiplication Property of
Inequality (Example)
Ex 3: Solve, graph, AND write the solution
set in interval notation:

a) 6x ≥ -18
b) -8y < 14
c) -z ≤ -6

Solving Inequalities Using
Both Properties

Solving Inequalities Using Both
Properties (Example)
Ex 4: Solve, graph, AND write the solution
set in interval notation:

a) -5x – 9 > -2x + 12
b) 4(y – 5) ≥ 3y – (y + 2)

Ex 5: Solve, graph, AND write the solution
set in interval notation:

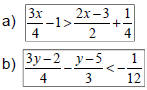
Summary
• After studying these slides, you should know
how to do the following:
– Graph an inequality on a number line
– Understand the Addition and Multiplication Properties
of Inequality
– Solve and graph inequalities

• Additional Practice
– See the list of suggested problems for 2.7

• Next lesson
– Solving Absolute Value Equations (Section E.1)