Partial Fractions Homework Solutions

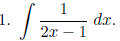
Hint. Let u = 2x − 1.
Let u = 2x − 1. Then du = 2 dx, and we get

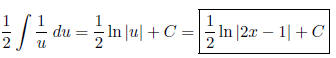
Moral. You can integrate anything that looks like !

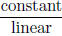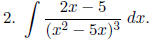
Hint. Let u = x² − 5x.
Let u = x² − 5x. Then du = 2x − 5 dx, and we get

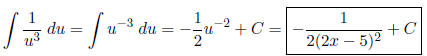
Moral. Always check to see if you can use u-substitution before trying anything fancy!

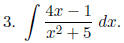
Hint. Split up the fraction, then use u-substitution (with u = x² + 5) on one term and the
following formula on the other:

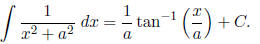
We have

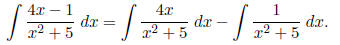
For the first term, let u = x² + 5. Then du = 2x dx, and the integral becomes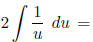
2 ln |u|+C = 2 ln |x²+5|+C. For the second term, use the formula with 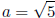. So the answer
to the original integral becomes

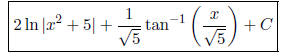
Moral: You can integrate anything that looks like

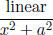
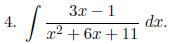
Hint. Complete the square in the denominator, i.e. x²+6x+11 = x²+6x+9+2 = (x+3)²+2.
Then let u = x + 3, and apply the technique in problem 3, above.

If u = x + 3 then x = u − 3. du = dx, so completing the square as in the hint, we have

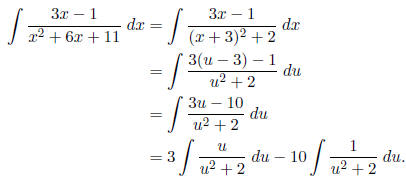
Now this looks just like the previous problem. Use u-substitution (or choose a different letter,
since we’re already in u) for the first term, and the inverse-tangent formula for the second; we get

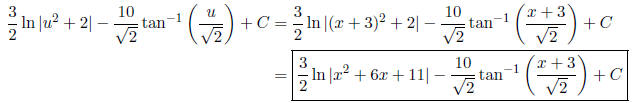
Moral: You can integrate anything that looks like   !

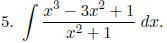
Hint. Perform polynomial division.
Check to make sure you get 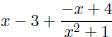. Integrate.

We verified this long division in class. Now we have

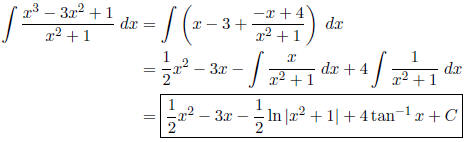
Moral. When the integrand is an improper rational function, perform polynomial division to
rewrite the quotient as a polynomial plus a proper rational function, then apply the previous
techniques.