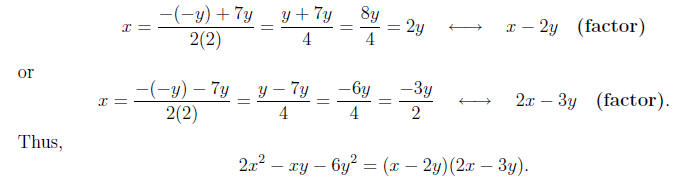Quadratic Formula
1 Introduction
The main intention of the quadratic formula is to find solutions to equations of the form
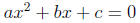
where a, b, and c are real numbers with a ≠ 0. The
quadratic formula tells you that, in
general, you have two such solutions and those solutions are:
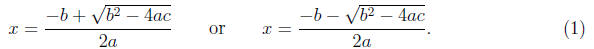
Actually you can use the quadratic formula for just about
anything involving polynomials
of degree 2 as long as you know how to look at it in the right way. We will use
the quadratic
formula for about three different types of problems:
(1) Factoring polynomials of the form ax^2 + bx + c.
[Sections 6.2-6.5]
(2) Solving equations of the form ax^2 + bx + c = 0 [Sections 6.6, 12.1,
12.2]
(3) Graphing equations of the form y = ax^2 + bx + c [Section 12.5]
2 Problem Type 1 - Factoring
Factoring, non-trivially, a quadratic means writing a
polynomial of degree 2 as a product of
two polynomials of degree 1. For example taking
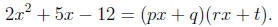
The real problem is how do you find the numbers for p, q,
r, and t which will actually
work. There are many trial-and-error methods which you can employ. With a little
practice,
for simple examples these can be quite fast. This shows the merit in the methods
demonstrated
in Sections 6.2-6.5 of our book. However, there is a way of computing these in a
straightforward manner.
We are actually able to factor any quadratic, but the
numbers for p, q, r, and t might
not be "nice". In our case, "nice" means that they are integers (whole numbers).
If they are
not, the we say that quadratic is prime or irreducible.
The direct way of finding the p, q, r, and t which will
factor is actually given by the
Quadratic Formula and the process involves three steps (actually 4, but step 0
is only a prep
stage that you won't have to do all the time). The steps are:
(0) Take out any factors which are common to all terms.
(1) Compute the discriminant

If the discriminant D is negative or not a perfect square,
then the quadratic is prime
and you stop. You can easily check whether or not D is a perfect square using
your
calculator.
(2) Find the roots from the quadratic formula:
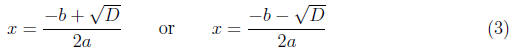
(3) Re-write the roots as factors. From the formulas, the
roots will look like fractions
x = p/q. In order to re-write them as factors, the denominator becomes the
coefficient
of x and you subtract the numerator.
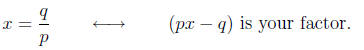
Important Idea. Remember that the important thing
is getting the correct association of
a, b, and c. If the term is being subtracted, then remember the coefficient is
negative. The
correspondence is:
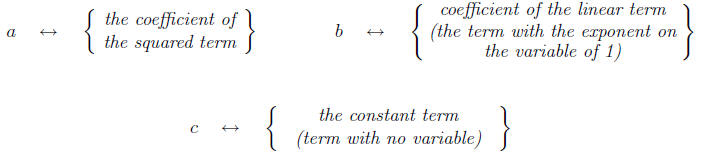
Example 1. Factor 20x^2 + 21x - 54.
Solution. Identifying a, b, and c, we have
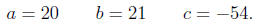
Computing the discriminant
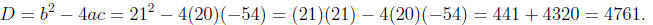
We can use the calculator as a check to see if 4761 is a
perfect square. Using the  -button
-button
on the calculator, we have
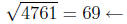 a whole number, so it
will factor
a whole number, so it
will factor
Calculating the roots
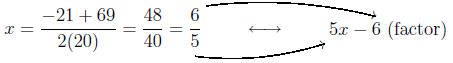
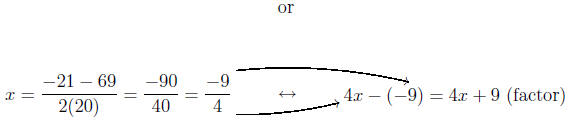
Thus, our factorization is
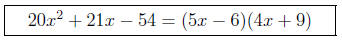
Checking this
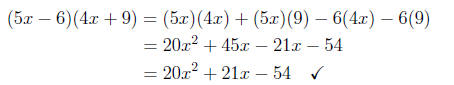
Example 2. Factor x^2 + 14x + 48.
Solution. We first have for a, b, and c
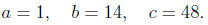
Then calculating the discriminant
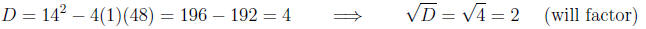
We then have

or

Thus
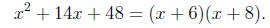
Example 3. Factor x^2 - 2x + 10.
Solution. Identifying a, b, and c, we have
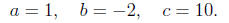
Calculating the discriminant
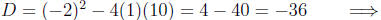 negative, so won't
factor
negative, so won't
factor
Thus,
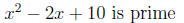
Example 4. Factor
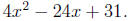
Solution. Identifying a, b, and c

Calculating the discriminant
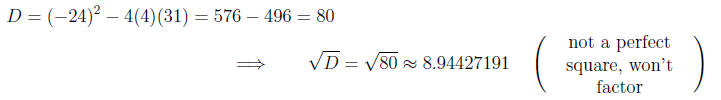
Thus,
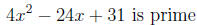
Example 5. Factor
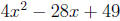
Solution. Identifying a, b, and c
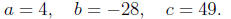
Calculating the discriminant
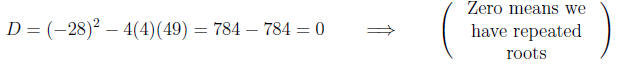
Calculating the roots and factors,
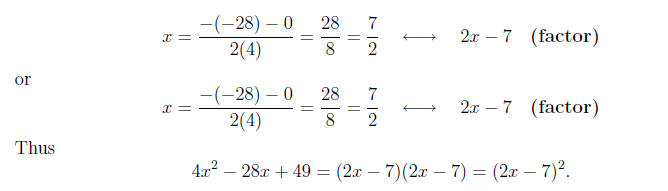
Example 6. Factor x^2 - 81.
Solution. We actually have
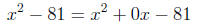
so identifying a, b, and c
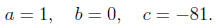
Calculating the discriminant
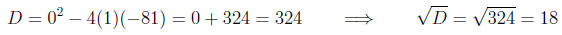 (will factor):
(will factor):
Calculating the roots and factors, we have
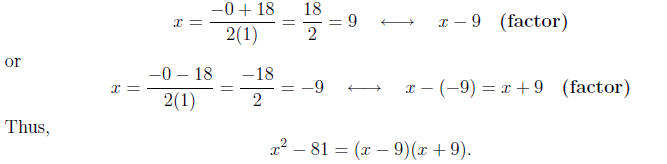
Actually, the difference of squares may be one of the few
times the special formulas from
section 6.5 are really useful as a short-cut in factoring. We have
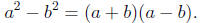
So in the previous example, if we recognize that 81 is a perfect square 81 = 9^2 then we have
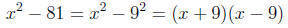
immediately. But as always, this is a short-cut and not really necessary.
Example 7. Factor
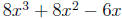
Solution. We first notice that each term has a factor of 2x in common. This means we have
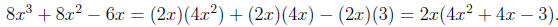
So we use the quadratic formula to factor 4x^2 + 4x - 3. Identifying a, b, and c
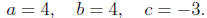
Calculating the discriminant
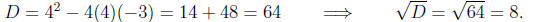
Calculating the roots and factors,
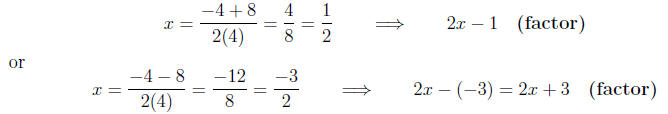
Thus, for our final answer we have
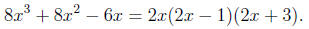
Example 8. Factor
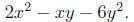
Solution. The idea is the same as before, but we treat y
just as if it were a number. Identifying
a, b, and c
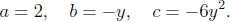
Calculating the discriminant
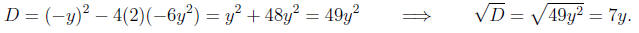
Note that
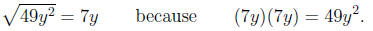
Calculating the roots and factors,