MATLAB : A TUTORIAL
1. Creating Vectors and Matrices
Row vectors: there are many ways of creating a vector
Explicit list
| >> x=[0 1 2 3 4 5]; | % What happens if you skip the semicolon? |
| >> x=[0,1,2,3,4,5]; | % Inserting commas doesnt change anything |
Using a:increment:b
| >> x= 0:0.2:1; | % same as x=[0 0.2 0.4 0.6 0.8], |
>> x= a: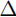 x:b; x:b;
|
% x=[a,a+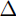 x,
a+2 x,
a+2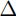 x,
a+3 x,
a+3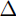 x,
. . . , b] x,
. . . , b]% that is, vector from a to b in increments of size 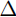 x x% What happens if 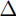 x
is not a integer divisor of b-a? x
is not a integer divisor of b-a? |
Using linspace(a,b,n)
| >> x= linspace(0,1,6); | % vector containing 6 points on interval [0,1] |
| >> a=0;b=1;n=6; | % Set variables |
| >> x= linspace(a,b,n); | % vector containing n points on interval [a,b] % Note: spacing is 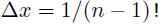 |
Using for loops
| >> for i=1:10 | % First example of a for loop. Note: 1:10=1:1:10 |
| >> x(i)=i; | % What happens if you skip semicolon?? |
| >> end | |
| >> a=0;b=1;n=10; delx=(b-a)/n; | % Set variables |
| >> for i=1:n+1 | |
| >> x(i)=a+delx*(i-1); | % index of x has to be an integer > 0 |
| >> end |
How long is the vector?
| >> length(x) | |
| >> d=size(x) | % What are the entries in the matrix d? |
Column vectors
Explicit list
>> x=[0;1;2;3;4]
Transposing a row vector
>> x=[0 1 2 3 4]’ % Vectors are matrices. A’=transpose(A)
Matrices
Explicit list
>> A=[1 1 1; 2 0 -1; 3 -1 2; 0 1 -1];
Special matrices
>> x=zeros(1,4), y=zeros(4,1)
>> x=ones(1,4), y=ones(4,1)
2. Evaluating functions y = f(x), manipulating vectors
Example
| >> x=0:0.1:1; | |
| >> y=sin(pi*x); | % Type help elfun to see a list of predefined functions |
Alternative, using a loop (much slower)
>> x=0:0.1:1;
>> n=length(x);
>> for i=1:n;
>> y(i)=sin(pi*x(i));
>> end;
Vectors are matrices
| >> y=x*x; | % What happens? Why? |
| >> x2=0:0.2:1; y=x+x2; | % What happens? Why? |
| >> y=x’*x | % What is y ? |
| >> y=x*x’ | % What is y ? |
Componentwise operation
| >> y=x.*x | % The dot denotes multiplication of components |
| >> y=x.^3 | % The carat denotes exponentiation |
| >> y=2*x | % Here you dont need a dot |
| >> y=1./x | % Here you do |
Accessing subvectors
| >> x=0:0.1:1; | |
| >> n=length(x) | |
| >> x2=x(5:10) | % What is x2? |
| >> x2=x([1,3,4,11]) | % What is x2? |
| >> x2=x(2:4:11) | % What is x2? |
Accessing submatrices
| >> a=[100 90 85; 117 110 108; 84 84 84; 96 90 88]; | |
| >> [m,n]=size(x) | |
| >> a2=a(2,3) | % What is the matrix a2? |
| >> a2=a(:,2) | % What is a2? |
| >> a2=a(2,:) | % What is a2? |
| >> a2=a(2:3,:) | % What is a2? |
| >> a2=a(2:3,[1,3]) | % What is a2? |
The sum command (type ’help sum’)
| >> y=[1,4,2,10]; sum(y); | % returns sum of all entries in vector y |
| >> sum(y(1:2:4)); | % what is it? |
| >> sum(a(:,1)); | % with a as before. what is it? |
3. Plotting
Plot command
| >> x=0:.1:1; y =sin(2*pi*x); | |
| >> plot(x,y); | % the two vectors have to have same dimensions |
Exercise:
| >> x=[0,1]; y=sin(2*pi*x); | |
| >> plot(x,y); | % What is going on?? |
Options
Line type options: -,:,--,-.
>> plot(x,y,’-’);
>> plot(x,y,’:’);
>> plot(x,y,’--’);
>> plot(x,y,’-.’);
Color options: y,m,c,r,g,b,w,k
>> plot(x,y,’g’); % green line (line is default)
>> plot(x,y,’r’)
Marker options: .,o,x,+,*,s,d,v,^,<,>,p,h (type help plot)
>> plot(x,y,’x’); % blue star (blue is default)
Using several options together
>> plot(x,y,’*-r’); % red line with star markers
Plotting several curves
>> x=0:0.05:1; y1=sin(2*pi*x); y2=cos(2*pi*x);
>> plot(x,y1,x,y2)
>> plot(x,y1,’-b’,x,y2,’--r’)
>> x=0:0.05:2; y1=x; y2=x.^2; y3=x.^3; y4=x.^4;
>> plot(x,y1,’-b’,x,y2,’--r’,x,y3,’*g’,x,y4,’-c’)
Alternative, using hold command
>> x=0:0.05:1; y1=sin(2*pi*x); y2=cos(2*pi*x);
>> plot(x,y1,’-b’)
>> hold on
>> plot(x,y2,’--r’)
>> hold off
The axis command
>> axis([0,2,0,4])
>> axis equal
>> axis square % Use ’help axis’ to see what other options there are
Labelling
>> xlabel(’time t’)
>> ylabel(’position s(t)’)
>> ylabel(’position s(t)’,’FontSize’,16)
>> title(’Its important to label your graphs!’)
>> text(0.6, 2,’some text’,’FontSize’,16)
>> set(gca,’FontSize’,16)
>> legend(’x’,’x^2’)
Simplest Plots
| >> plot(x) | % Plots x vs its index, quick way to see what is in x |
| >> plot(x1,x2) | % Careful! This does not plot x1 vs index |
| >> | % and x2 vs index. Instead, plots x2 vx x1 |
| >> plot(x1,x2,x3) | % and this gives you an error. Why? |
4. Miscellaneous commands
Comments
>> % This is a comment
The help and lookfor commands
| >> help zeros | % you need to know exact command name |
| >> help for | |
| >> help | % lists topics for which there is help |
| >> lookfor factorial | % if you do not know the exact command name |
The print command
| % prints current figure to current printer | |
| >> print -deps | % prints current figure to .eps file |
| >> print -depsc | % prints current figure to color .eps file |
| >> print -dps | % prints current figure to .ps file |
The pause command
| >> pause | % What does this do? |
| >> pause(2) | % What does this do? |
The continuation symbol
| >> x=[0 1 2 3 4 5 ... | % To continue the current command |
| >> 6 7 8 9 10] | % to the next line, use ... |
The hold command (see example in §3)
Further example, plot circle from
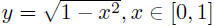 (vL
P1.2.3)
(vL
P1.2.3)
The clear command
| >> clear | % clears all variables from memory |
| >> clear x y ... | % clears listed variables from memory |
The clf command
>> clf % clears current figure
5. Scripts
You can type a string of commands into a file whose name ends in .m, for
example
‘flnm.m’. If you then type
>> flnm
in your matlab window, it executes all the commands in the file flnm.m.
Make sure you document your script files! Add a few lines of comments that state
what
the script does.
6. Saving your work
Save all your script files on a floppy or CD-RW, preferably organized in
directories
(folders).
At the beginning of each in-class-programming session, transfer all necessary
files or
directories from your floppy (or from another UNM account using FsecureSSH) onto
the
local working directory.
In DSH 141, use E: as your working directory.
In ESCP 110, use Temp: as your working directory.
7. Timing your code, the commands tic,toc
| >> tic | % starts stopwatch |
| >> statements | |
| >> toc | % reads stopwatch |
Exercise: Find out how much faster the vector operation
>> x=0:0.01:1;
is than the following statement of componentwise operations
>> for j=1:101;
>> x(j)=(j-1)*0.01;
>> end;
Answer: (using old version of matlab) about 50 times faster! ) MATLAB VECTORIZES
8. The for statement
>> % The command for repeats statements for a specific number of times.
>> % The general form of the while statement is
>>
>> FOR variable=expr
>> statements
>> END
>>
>> % expr is often of the form i0:j0 or i0:l:j0.
>> % Negative steps l are allowed
Example 1: What does this code do?
>> n = 10;
>> for i=1:n
>> for j=1:n
>> a(i,j) = 1/(i+j-1);
>> end
>> end
9. The if statement
>> % The general form of the if statement is
>>
>> IF expression
>> statement
>> ELSEIF expression
>> statement
>> ELSE expression
>> statement
>> END
>>
>> % where the ELSE and ELSEIF parts are optional.
>> % The expression is usually of the form
>> % a oper b
>> % where oper is == (equal), <, >, <=, >=, or ~= (not equal).
Example 1: What does this code do?
>> n=10;
>> for i=1:n
>> for j=1:n
>> if i == j
>> A(i,j) = 2;
>> elseif abs(i-j) == 1
>> A(i,j) = -1;
>> else
>> A(i,j) = 0;
>> end
>> end
>> end
Exercise 2: Define up-down sequence
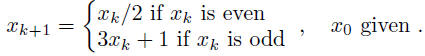
Write a script that builds the up-down sequence for k≤200.
Plot the solution vector x(k), k = 1, . . . , 200, for several initial
conditions.
>> % You can also combine two expressions
>> % with the and, or, and not operations.
>> %
>> % expression oper2 expression
>> %
>> % where oper2 is & (and), | (or), ~ (not).
Example 3: What does this code do?
>> for i=1:10
>> if (i > 5) & (rem(i,2)==0)
>> x(i)=1;
>> else
>> x(i)=0;
>> end
>> end
10. The while statement
>> % The command while repeats statements an indefinite number of times,
>> % as long as a given expression is true.
>> % The general form of the while statement is
>>
>> WHILE expression
>> statement
>> END
>>
Example 1: What does this code do?
>> x = 4;
>> y = 1;
>> n = 1;
>> while n<= 10;
>> y = y + x^n/factorial(n);
>> n = n+1;
>> end
Remember to initialize n and update its value in the loop!
Exercise 2: For the up-down sequence
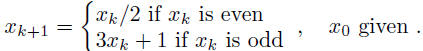
Write a script that builds the up-down sequence while x(k) ≠
1
and k≤200, using the WHILE statement.
Plot the solution vector x(k), k = 1, . . . , 200, for several initial
conditions.
11. MATLAB Functions
MATLAB Functions are similar to functions in Fortran or C. They enable us to
write
the code more efficiently, and in a more readable manner.
The code for a MATLAB function must be placed in a separate .m file having
the same
name as the function. The general structure for the function is
function hOutput parametersi = hName of Functioni (hInput Parametersi)
%
%
% Comments that completely specify the function
%
hfunction bodyi
A function is called by typing
>> variable = hName of Functioni
When writing a function, the following rules must be followed:
• Somewhere in the function body the desired value must be assigned to the
output
variable!
• Comments that completely specify the function should be given immediately
after
the function statement. The specification should describe the output and detail
all
input value assumptions.
• The lead block of comments after the function statement is displayed when the
function is probed using help.
• All variables inside the function are local and are not part of the MATLAB
workspace
Exercise 1: Write a function with input parameters x and n that evaluates the
nth order Taylor approximation of ex. Write a script that calls the
function for various values of n and plots the error in the approximation.
Solution: The following code is written in a file called ApproxExp.m:
function y=ApproxExp(x,n);
| % Output parameter: | y (nth order Taylor approximation of ex) |
| % Input parameters: | x (scalar) |
| % | n (integer) |
sumo = 1;
for k=1:n
sumo = sumo + x^k/factorial(k);
end
y = sumo;
A script that references the above function and plots approximation error is:
x=4;
for n=1:10
z(n) =ApproxExp(x,n)
end
exact=exp(4)
plot(abs(exact-z))
Exercise 2: Write the function ApproxExp more efficiently.
Exercise 3: Do the same as Exercises 1 and 2, but let x and y be vectors.
Example 4: An example of a function that outputs more than
one variable. The
function computes the approximate derivative of function fname, the
error in the approximation, and the estimated error.
The following code is written in a file called MyDeriv.m:
function [d,err,esterr]=MyDeriv(fname,dfname,a,h,M,eps);
| % Output parameter: | d (approximate derivative using |
| % | finite difference (f(h+h)-f(a))/h) |
| % | err (approximation error) |
| % | err (estimated approximation error) |
| % Input parameters: | fname (name of function) |
| % | dfname (name of derivative function) |
| % | a (point at which derivative approx) |
| % | h (stepsize) |
| % | M (upper bound on second derivative) |
| % | eps (error in f(a+h)-f(a)) |
d = (feval(fname,a+h)-feval(fname,a))/h;
err = abs(d-feval(dfname,a));
esterr = h/2*M+2*eps/h;
A script that references the above function and plots the
approximation error
and the estimated error is:
a=1; M=1; eps=10^(-15);
h=logspace(-1,-16,16);
n=length(h);
for i=1:n
[d(i),err(i),esterr(i)]=MyDeriv(’sin’,’cos’,a,h(i),M,eps);
end
loglog(h,err)
Exercise 5:
| What happens if you call | >> d=MyDeriv(fname,dfname,a,h,M,eps) |
| or simply? | >> MyDeriv(fname,dfname,a,h,M,eps) |
Example 5: An example showing how to call a function whose
input is a user defined
function, instead of a function implicitely defined in MATLAB,
such as the ’sin’ function used in the previous example.
This MATLAB function (in file MyPlot.m) plots the function
fname
on an interval from a to b using n points (no output variables). We
then call it to plot y = x^2 on [0, 2] using 100 points.
function MyPlot(fname,a,b,n);
| % Input parameters: | fname (name of function) |
| % | a,b (endpoint of interval on x-axis) |
| % | n (number of points in [a,b]) |
x = linspace(a,b,n);
y = feval(fname,x);
plot(x,y)
To call the above function type
and the estimated error is:
MyPlot(’f1’,0,2,100);
where f1 is a user specified function! That is, you need
to write the function that
evaluates f1 at x (in file f1.m):
function y=f1(x);
| % Input parameters: | fname (name of function) |
| % | x (vector) |
| % Output parameter: | y (=f(x)) |
y = x.^2;
12. Matrix operations
Defining matrices, an example
>> A=[ 1 2 3 4; -1 2 3 1; 1 1 1 1 ] % What does this do?
Special matrices
>> eye(n) % returns nxn identity matrix
Matrix Multiplication
| >> C=A*B | % multiplies matrix A by matrix B provided |
| >> | % dimensionally correct (# columns of A=# rows of B) |
Inverses and determinants
| >> B=inv(A) | % returns inverse of A |
| >> d=det(A) | % returns determinant of A |
| >> A/B | % equals A* inv B |
Solving systems
>> A\b % returns solution to Ax=b


