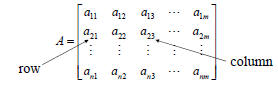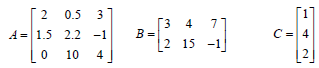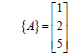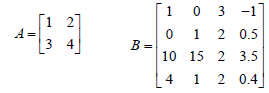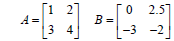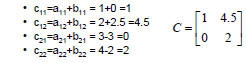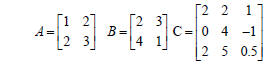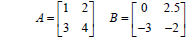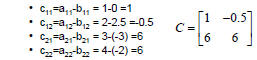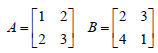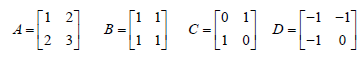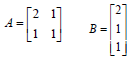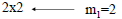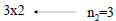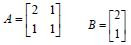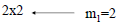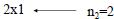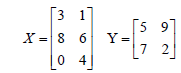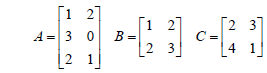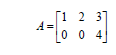Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Matrix and Vector Operations

Learning Objectives
• Lesson 1:
– Define matrices
– Distinguish vectors and matrices
– Identify square matrices
– Perform basic matrix operations
• Sum/subtraction
• Multiply matrices

Review of
Matrices
– Definition
– Types of
matrices
– Matrix operations

Matrix Definition

• Array of numbers that can be represented
in the following form:

• Where “n” represents the row number
• Where “m” represents the column
number
• Matrix A has dimensions (n x m)

Exercise 1

• Given the following matrices, identify the
dimensions of each matrix, what is the
value of the following elements a₁₂, a₂₁,
a₃₂,a₂₂

Review of
Matrices
– Definition
– Types of
matrices
– Matrix operations

Types of Matrices

• There are different types of
important matrices in linear algebra

• However, for the purpose of this
course we will focus on:
– Vectors
– Square matrices

Vectors

• Vectors are type of matrices that have
either one row or one column

• Matrices with one column (m=1) are
called column vectors, e.g.,

• Matrices with one row (n=1) are called
row vectors, e.g.,
{B} = [1 2 3]

Square matrices

• If m=n, we have a square matrix,
eg:

Matrix Operations

• Addition:
– Matrices can be added only if they have the
same dimensions
– To add matrices each element must be
added
– Steps for adding matrices:

• Identify the dimensions of the matrices
• If the dimensions are not the same the matrices
can’t be added
• If the dimensions are the same the matrices can
be added by adding each of the individual
elements

Example Adding Matrices • Given A and B, calculate C= A+B • Procedure: – Dimensions of A: 2×2, Dimensions of B: 2×2 – Because both matrices have the same dimensions they can be added – Elements of C matrix:
Exercise 2 • Given the matrices, A, B, and C obtain matrix D = A + B and E=B+C
Review of Matrices – Definition – Types of matrices – Matrix operations	Matrix Operations • Subtraction: – Matrices can be subtracted only if they have the same dimensions – To subtract matrices each element must be subtracted – Steps for subtracting matrices: • Identify the dimensions of the matrices • If the dimensions are not the same the matrices can’t be subtracted • If the dimensions are the same the matrices can be subtracted by subtracting each of the individual elements
Example Subtracting Matrices • Given A and B, calculate C= A-B • Procedure: – Dimensions of A: 2×2, Dimensions of B: 2×2 – Because both matrices have the same dimensions they can be subtracted – Elements of C matrix:
Exercise 3 • Given the matrices, A and B, obtain matrix C = A - B
Review of Matrices – Definition – Types of matrices – Matrix operations	Matrix Operations • Multiplication of a matrix by a scalar: – If “g” is a scalar, a matrix “A” can be multiply by “g” – To do this, we need to multiply each element of matrix “A” by the scalar “g” – See procedure below:

Exercise 4 • Given the matrices A, B, C, D • Perform the following calculations – F=A- B+0.5D – G=2(A+B+C)- D
Review of Matrices – Definition – Types of matrices – Matrix operations	Matrix Operations
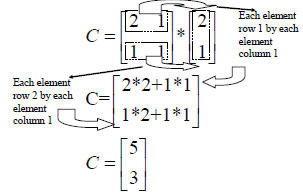
	• Product of two matrices – The number of columns in the first matrix(m₁), must be equal to the number of rows in the second matrix (n₂). If the conditions given above are not true, the two matrices can’t be multiply – The new matrix will have dimensions: n₁m₂ – Multiply each element of the row of the first matrix, by each element of the column of the second matrix and add them. This operation will generate the new elements of the product matrix
• Given Matrices A and B, calculate C=A*B Solution: Dimensions of A: Dimensions of B: Because m₁ is different to n₂ the product can’t be done
• Given Matrices A and B, calculate C=A*B Solution: Dimensions of A: Dimensions of B: Because m₁ is equal to n₂ the product CAN be done. The new matrix C will have dimensions 2x1
Solution Example Continues
Exercise 5 • Given the matrices X and Y, calculate the matrix P = X Y
Review of Matrices – Definition – Types of matrices – Matrix operations	Matrix Operations • Operations of product of matrices – The product of two matrices is not commutative AB ≠ BA – The product of matrices is associative ( AB)C = A(BC) – The product of matrices is distributive A(B +C) = ( AB) + ( AC)
Exercise 6 • Given the matrices A, B, and C, and the scalar g=2. Perform the following computation: D = g*A(B+C)
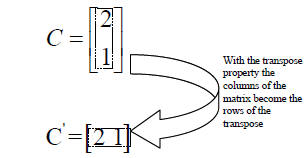
Review of Matrices – Definition – Types of matrices – Matrix operations	Matrix Operations • Transpose – The transpose “A^T” of a matrix “A” transforms rows into columns – Given a matrix “A”, the transpose matrix “A^T” is the matrix in which a_ij of the transpose is a_ji of the original matrix
Solution Example Continues
Exercise 7 • Given matrix A, calculate the transpose of A
Summary • Can you define a matrix? • Can you identify a particular element in a matrix? • What are square matrices? • What are vectors? • Can you – Add matrices – Subtract matrices – Multiply matrices (remember product properties) – Calculate transpose of matrices