MATH PROBLEM SET 1

Key: (E) denotes easy. If you honestly feel the problem is too easy, just write
"okay", but try to solve some harder problems as well.

1.1)(E) Prove the Division Theorem: If a ≥ b > 0 are integers, then there exist
unique non-negative integers q and r such that a = qb + r and 0 ≤ r < b. Hint:
It suffices to take q to be the largest non-negative integer such that a − qb ≥ 0.

1.2)(E) In the notation of Problem 1.1), show that b|a 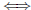r = 0.

1.3) Prove the converse of Euclid's Lemma: suppose d is a positive integer such
that whenever d|ab, d|a or d|b. Then d is prime.

Remark: Among other things, this allows us to generalize the notion of primes
to not-necessarily principal ideals.

1.4)a)(E) "To contain is to divide": for integers a and b, we have .
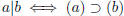b) Confirm that part a) holds true for elements a and b in any commutative ring.
c) For elements a, b in an integral domain R, show that the following are equivalent:
(i) There exists a unit 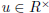such that b = ua.
(ii) There exist units 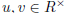such that b = ua, a = vb.
(iii) a | b and b | a.
(iv) There is an equality of principal ideals (a) = (b).
d)* Find a commutative ring R (not an integral domain) and elements a and b such
that in part c) above, (iii) and (iv) hold but (i) and (ii) do not. In other words, in
a general commutative ring, being associates is a stronger relation than generating
the same principal ideal.

1.5) Prove or disprove: The gcd(0, 0) does not exist. In other words, when a = b = 0,
there is no integer d such that for all integers e, if e | a & e | b, then e | d.

The next exercise concerns the rng E = 2Z of all even integers.

1.6) Give a necessary and sufficient condition on a positive element x ∈ E to have
two different factorizations into positive E-primes. Hint: pay attention to
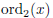
and also to the number of odd primes dividing x.

1.7) Prove Proposition 12 , about
the basic properties of the 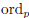functions.

1.8) Complete the proof that 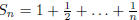is never an integer by showing
that for all n ≥1, .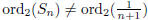

1.9)** Show that except for n = 1, 2, 6, the decimal expansion of 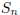is nonterminating.
(I.e., show that except for these values, 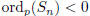for some prime
p ≠ 2, 5.)

1.10) For any nonzero integers a and b, show that

gcd(a, b) · lcm(a, b) = ab.

1.11) For integers a and b, show that the intersection of the two ideals (a) ∩ (b)
is an ideal of Z. In fact, if you know the definition of an ideal in a commutative
ring, show that the intersection of any two (or more. . .) ideals is always an ideal.3
Because Z is a PID, we must have (a) ∩ (b) = (c) for some c ∈ Z, well-determined
up to a sign. What is c in terms of a and b?

1.11.5) a) Let 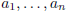be a (finite) set of integers. Define the greatest common
divisor gcd(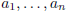) of the set, and show that it exists and is unique up to
a sign. In fact, show that the set



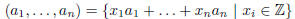
is an ideal of Z, and that the positive generator of this (necessarily principal!) ideal
is the gcd we are looking for.
b) Define lcm(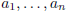), show it exists, and explain how to get it from the ideals


1.12) Show that .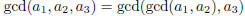

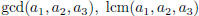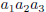2.13)* Find an identity relating and . Can
you extend this to more than three numbers? (Hint: inclusion/exclusion.)

1.14) One says that a set of integers 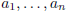is relatively prime in pairs
if for all i ≠ j, .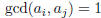

a) Show that if 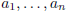are relatively prime in pairs, then gcd(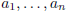) = 1.
b) Show that the converse does not hold when n ≥ 3: indeed, find the smallest
example of three integers which are not simultaneously divisible by any d > 1 but
for which any two have a nontrivial common divisor.

Remark: The phrase "let 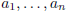be relatively prime integers" is therefore ambiguous
when n ≥ 3. Probably it ought to mean the weaker condition that
gcd(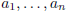) = 1 but careful authors rephrase to avoid the ambiguity. If you
hear someone say it, stop and ask them which one they mean!

1.15) Prove the rational roots theorem: if



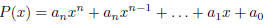
is a polynomial with integer coefficients, the only possible rational roots are of the
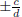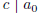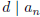form where and . Explain how this gives yet another proof of, e.g.,
the irrationality of .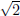

1.16) a) Show that 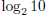is irrational.
b)* Let a, b ∈ 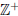. Give a criterion for the irrationality of .

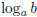G1.1) Let F be a field and let 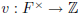be a surjective map satisfying properties
a) and b) of Proposition 12; v is said to be a discrete valuation of F.
a) Let 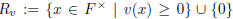 . Show that 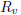is a subring of F, the
valuation ring. (It is common to formally set v(0) = ∞ to avoid having to keep
"manually inserting 0.")
b) Since v is surjective, there is an element π ∈ 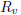with v( π) = 1. Show that for
any n ≥1,



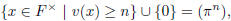
the principal ideal of 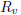generated by 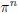(of course π⁰ = 1).

c) Show that every ideal of 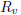is of the form ( πⁿ) for a suitable n ∈ N. In particular,
every ideal of 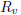is principal, and there is a unique maximal ideal, (π ).

d) When F = Q, 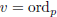, what is the valuation ring ?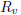

e) Suppose k is a field, and consider F = k(t), the quotient field of the ring of
polynomials k[t] with coefficients in k. Show that the map v which takes a rational
function 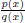to deg(q(x))−deg(p(x)) is a discrete valuation of k(t). Note that this
is consistent with our previous convention that the degree of the zero polynomial
is −∞!